上一篇,我们通过一个项目讲解了“实战 5 步”的前两步。在第一步“定义问题”中,我们定义了要处理的问题,也就是根据点赞数和转发数等指标,估计一篇文章能实现多大的浏览量。同时我们还将它归类为回归问题;在第二步“收集数据和预处理”中,我们做好了数据的预处理工作,还把数据集拆分成了这四个数据集:
- 特征训练集(X_train)
- 特征测试集(X_test)
- 标签训练集(y_train)
- 标签测试集(y_test)
有了这些数据集后,我们就可以开始考虑选什么算法,然后建立模型了。所以,这篇文章我们继续完成后三步:
-
选择算法并建立模型
-
训练拟合模型
-
评估并优化模型性能
来把这个项目做完。下面,我们先看看怎么选择算法并建立模型。
第 3 步 选择算法并建立模型
在这一步中,我们需要先根据特征和标签之间的关系,选出一个合适的算法,并找到与之对应的合适的算法包,然后通过调用这个算法包来建立模型。
选算法的过程很考验数据科学家们的经验,不过,你也无需担心自己没有经验,在这个课程中,我会给你讲清楚每一个实战中所用的算法的原理,帮助你建立起选算法的直觉。
具体到我们这个项目里,在上一讲中我说过,我们这个数据集里的某些特征和标签之间,存在着近似线性的关系。而且,这个数据集的标签是连续变量,因此,适合用回归分析来寻找从特征到标签的预测函数。
所谓回归分析 (regression analysis),就是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析,说白了就是当自变量变化的时候,研究一下因变量是怎么跟着变化的,它可以用来预测客流量、降雨量、销售量等。
不过,回归分析的算法有很多种,比如说线性回归,多项式回归,贝叶斯回归等等,那具体该选哪个呢?其实,这是根据特征和标签之间的关系来决定的。我们在上一篇的可视化过程中,推测特征和标签可能存在线性关系,并且用下面这个散点图简单做了验证。

所以这里,我们就选择用线性回归算法来建模。
线性回归算法是最简单、最基础的机器学习算法,它其实就是给每一个特征变量找参数的过程。我想你一定熟悉一元线性回归的公式:
$$
y = ax + b
$$
对于一元线性回归来说,它的内部参数就是未知的斜率和截距。只不过在机器学习中,我们把斜率 a 叫做权重(weight),用英文字母 w 代表,把截距 b 叫做偏置(bias),用英文字母 b 代表。所以机器学习中一元线性回归的公式也写成:
$$
y = wx + b
$$
而在我们这个项目中,数据集中有 4 个特征,所以就是:
$$
y = w_1x_1+w_2x_2+w_3x_3+w_4x_4+b
$$
因此,我们的模型就会有 5 个内部参数,也就是 4 个特征的权重和一个偏置(截距)需要确定。不过这些公式的具体代码实现,都不用我们自己完成,它们全部封装在工具包里了。你只要对算法的原理有个印象就行了。
确定好算法后,我们接着来看一下调用什么样的算法包建立模型比较合适。
对于机器学习来说,最常用的算法工具包是 scikit-learn,简称 sklearn,它是使用最广泛的开源 Python 机器学习库,堪称机器学习神器。sklearn 提供了大量用于数据挖掘的机器学习工具,覆盖数据预处理、可视化、交叉验证和多种机器学习算法。
虽然我们已经选定使用线性回归算法,但是在 sklearn 中又有很多线性回归算法包,比如说基本的线性回归算法 LinearRegression,以及在它的基础上衍生出来的 Lasso 回归和 Ridge 回归等。
那哪一个才是适合我们这个项目的算法包呢?其实,我们一般选算法包的方法是从能够解决该问题的最简单的算法开始尝试,直到得到满意的结果为止。对于这个项目,我们选择 LinearRegression,它也是机器学习中最常见、最基础的回归算法包。其它回归算法包,未来我会慢慢给你介绍。
调用 LinearRegression 建立模型非常简单,两行代码就可以搞定:
from sklearn.linear_model import LinearRegression # 导入线性回归算法模型
linereg_model = LinearRegression() # 使用线性回归算法创建模型可以看到,我把这个线性回归模型命名为了“linereg_model”。那到这里,我们算不算是建立好模型了呢?是的,模型已经创建出来了,我们可以开始训练它了。不过,有一点需要指出,建立模型时,你通常还需要了解它有哪些外部参数,同时指定好它的外部参数的值。
模型的参数有两种:
- 内部参数:内部参数是属于算法本身的一部分,不用我们人工来确定,刚才提到的权重 w 和截距 b,都是线性回归模型的内部参数;
- 外部参数:而外部参数也叫做超参数,它们的值是在创建模型时由我们自己设定的。
对于 LinearRegression 模型来讲,它的外部参数主要包括两个布尔值:
-
fit_intercept ,默认值为 True,代表是否计算模型的截距。
-
normalize,默认值为 False,代表是否对特征 X 在回归之前做规范化。
不过呢,对于比较简单的模型来说,默认的外部参数设置也都是不错的选择,所以,我们不显式指定外部参数而直接调用模型,也是可以的。在上面的代码中,我就是在创建模型时直接使用了外部参数的默认值。
还有一点需要说明的是,我们文章中不会去详细介绍每一个参数的意义,因为这不是我们的重点。但是对于一些特殊情况下需要调整外部参数的,在后面的文章里我会告诉你调参的重要技巧。
好,现在我们已经创建好线性回归模型 linereg_model,接下来我们就可以进入机器学习的核心环节“训练拟合机器学习模型”了。
第 4 步 训练模型
训练模型就是用训练集中的特征变量和已知标签,根据当前样本的损失大小来逐渐拟合函数,确定最优的内部参数,最后完成模型。虽然看起来挺复杂,但这些步骤,我们都通过调用 fit 方法来完成。
fit 方法是机器学习的核心环节,里面封装了很多具体的机器学习核心算法,我们只需要把特征训练数据集和标签训练数据集,同时作为参数传进 fit 方法就行了。
linereg_model.fit(X_train, y_train) # 用训练集数据,训练机器,拟合函数,确定内部参数运行该语句后的输出如下:
LinearRegression()这样,我们就完成了对模型的训练。你可能会觉得很奇怪,既然训练模型是机器学习的核心环节,怎么只有一句代码?其实这就是我反复强调过的,由于优秀的机器学习库的存在,我们可以用一两行语句实现很强大的功能。所以,不要小看上面那个简单的 fit 语句,这是模型进行自我学习的关键过程。
在这个过程里,fit 的核心就是减少损失,使函数对特征到标签的模拟越来越贴切。那么它具体是怎么减少损失呢?这里我画了一张图片展示模型从很不靠谱到比较靠谱的过程。

这个拟合的过程,同时也是机器学习算法优化其内部参数的过程。而优化参数的关键就是减小损失。
那什么是损失(loss)呢?它其实是对糟糕预测的惩罚,同时也是对模型好坏的度量。损失也就是模型的误差,也称为成本或代价。名字虽多,但都是一个意思,就是当前预测值和真实值之间的差距的体现。它是一个数值,表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确,则损失为 0;如果不准确,就有损失。
在机器学习中,我们追求的当然是比较小的损失。不过,模型好不好,还不能仅看单个样本,还要针对所有数据样本,找到一组平均损失“较小”的函数模型。样本的损失大小,从几何意义上基本可以理解为预测值和真值之间的几何距离。平均距离越大,说明误差越大,模型越离谱。在下面这个图中,左边是平均损失较大的模型,右边是平均损失较小的模型,模型所有数据点的平均损失很明显大过右边模型。

因此,针对每一组不同的参数,机器都会基于样本数据集,用损失函数算一次平均损失。而机器学习的最优化过程,就是逐步减小训练集上损失的过程。具体到我们今天这个回归模型的拟合,它的关键环节就是通过梯度下降,逐步优化模型的参数,使训练集误差值达到最小。这也就是我们刚才讲的那个 fit 语句所要实现的最优化过程。
在这里面,线性回归中计算误差的方法很好理解,就是数据集中真值与预测值之间的残差平方和。那梯度下降又是怎么一回事呢?为了让你直观地理解,我用一张图来展示一下,梯度下降是怎么一步一步地走到损失曲线中的最小损失点的。

就像图里这样,梯度下降其实就和下山一样。你可以想象一下,当你站在高处,你的目标就是找到一系列的参数,让训练数据集上的损失值最小。那么你该往哪走才能保证损失值最小呢?关键就是通过求导的方法,找到每一步的方向,确保总是往更小的损失方向前进。
所以,你可以看出方向是有多么的重要。机器学习最优化之所以能够拟合出最佳的模型,就是因为能够找到前进方向,你看,不仅我们人需要方向,连 AI 也需要正确的方向。
关于梯度下降,你理解这些就已经差不多了。至于具体的细节,我们在这个文章中并不会通过公式和代码实现,这也是基于不重复造轮子的原则。那到这里为止,我们已经完成了模型的建立和训练,接下来,我们一起看看怎么对这个训练好的模型进行评估和优化,让它尽可能精准地估计出我们的文章浏览量。
第 5 步 模型的评估和优化
我们刚才说,梯度下降是在用训练集拟合模型时最小化误差,这时候算法调整的是模型的内部参数。而在验证集或者测试集进行模型效果评估的过程中,我们则是通过最小化误差来实现超参数(模型外部参数)的优化。
对此,机器学习工具包(如 scikit-learn)中都会提供常用的工具和指标,对验证集和测试集进行评估,进而计算当前的误差。比如 R2 或者 MSE 均方误差指标,就可以用于评估回归分析模型的优劣。
不过呢,在开始评估模型之前,我想请你思考一下:在我们这 5 个实战步骤里面,并没有“使用模型预测浏览量”这个环节,这是为什么呢?其实这个环节已经包含在第 5 步“模型性能的评估和优化”之中了,并且是我们在第 5 步中首先要去实现的。
具体来说,在“模型的评估和优化”这一步中,当我们预测完测试集的浏览量后,我们要再拿这个预测结果去和测试集已有的真值去比较,这样才能够求出模型的性能。而这整个过程也同样是一个循环迭代的过程,我把这个循环过程总结成了下面的图,你可以看看:

对于我们这个项目来说,预测测试集的浏览量,只需要用训练好的模型 linereg_model 中的 predict 方法,在 X_test(特征测试集)上进行预测,这个方法就会返回对测试集的预测结果。
y_pred = linereg_model.predict(X_test) #预测测试集的Y值在几乎所有的机器学习项目中,你都可以用 predict 方法来进行预测,它就是用模型在任意的同类型数据集上去预测真值的,可以应用于验证集、测试集,当然也可以应用于训练集本身。
这里我要说明一下,为了简化流程,我们并没有真正进行验证和测试的多重循环。因此,在这个项目中,X_test 既充当了测试集,也充当了验证集。
拿到预测结果后,我们再通过下面的代码,把测试数据集的原始特征数据、原始标签真值,以及模型对标签的预测值组合在一起进行显示、比较。
df_ads_pred = X_test.copy() # 测试集特征数据
df_ads_pred['浏览量真值'] = y_test # 测试集标签真值
df_ads_pred['浏览量预测值'] = y_pred # 测试集标签预测值
df_ads_pred #显示数据输出结果如下:

可以看出,浏览量预测值是比较接近于真值的。而且对于一些文章,这个模型的预测得非常准确,比如编号第 1387 号数据,其实际浏览量为 213501,预测浏览量为 216491。这就是一个很棒的结果。
如果你想看看现在的模型长得什么样?你可以通过 LinearRegression 的 coef_ 和 intercept_ 属性打印出各个特征的权重和模型的偏置来。它们也就是模型的内部参数。
print('当前模型的4个特征的权重分别是: ', linereg_model.coef_)
print('当前模型的截距(偏置)是: ', linereg_model.intercept_)输出如下:
当前模型的4个特征的权重分别是: [ 48.08395224 34.73062229 29730.13312489 2949.62196343]
当前模型的截距(偏置)是: -127493.90606857178这也就是说,我们现在的模型的线性回归公式是:
$$
yy=48.08x_1(点赞) + 34.73x_2(转发) + 29730.13x_3(热度) + 2949.62x_4(评级) - 127493.91
$$
不过到这里,整个机器学习项目并没有结束,我们最后还要给出当前这个模型的评估分数:
print("线性回归预测评分:", linereg_model.score(X_test, y_test)) # 评估模型在机器学习中,常用于评估回归分析模型的指标有两种:$$ R^2 $$ 分数和 MSE 指标,并且大多数机器学习工具包中都会提供相关的工具。对此,你无需做过多了解,只需要知道我们这里的 score 这个 API 中,选用的是 $$ R^2 $$ 分数来评估模型的就可以了。
最后我们得到这样的结果:
线性回归预测评分: 0.7085754407718876可以看到,$$ R^2$$ 值约为 0.708。那这意味着什么呢?
一般来说,$$ R^2$$ 的取值在 0 到 1 之间,$$ R^2$$ 越大,说明所拟合的回归模型越优。现在我们得到的 $$ R^2$$ 值约为 0.708,在没有与其它模型进行比较之前,我们实际上也没法确定它是否能令人满意。
因为分数的高低,与数据集预测的难易程度、模型的类型和参数都有关系。而且,R2 分数也不是线性回归模型唯一的评估标准。关于模型的评估和优化,我们就先讲到这里,更多内容,我们还会在以后逐步深入讲解。
不过你需要知道的是,如果模型的评估分数不理想,我们就需要回到第 3 步,调整模型的外部参数,重新训练模型。要是得到的结果依旧不理想,那我们就要考虑选择其他算法,创建全新的模型了。如果很不幸,新模型的效果还是不好的话,我们就得回到第 2 步,看看是不是数据出了问题。

这也是为什么,我一直强调机器学习项目是一个循环迭代的过程,优秀的模型都是一次次迭代的产物。
当模型通过了评估,就可以去解决实际问题了,机器学习项目也算是基本结束。你或许会问,为什么“实战 5 步”中没有模型的上线和部署?这是因为在通常的机器学习项目中,机器学习工程师并不负责这一块,而且,各个公司把机器学习部署到生产环境的方法也大不相同。所以,我们没有把部署模型放在我们的实战 5 步里。不过,具体怎么部署模型,我在后面会讲到。
总结
这一讲的内容到此就全部结束了,现在你已经拥有了一次完整的机器学习实战经历。怎么样,并没有你想象得那么难吧?
在这一讲和上一讲中,我们通过一个预测软文浏览量的实战项目,了解了机器学习项目要经历 5 个步骤。
- 第一步就是通过定义问题来明确我们的项目目标;
- 第二步是数据的收集和预处理,这一步的重点是把数据转换成机器学习可处理的格式,这样我们就可以在
- 第三步中针对问题选定适宜的算法,来建立模型了。
有了模型后,我们要在接下来的
- 第四步中训练模型、拟合函数。
- 最后,再对训练好的模型进行评估和优化。对于这最后一步,也就是第 5 步,我们的重点是反复测评,找到最优的超参数,确定最终模型。
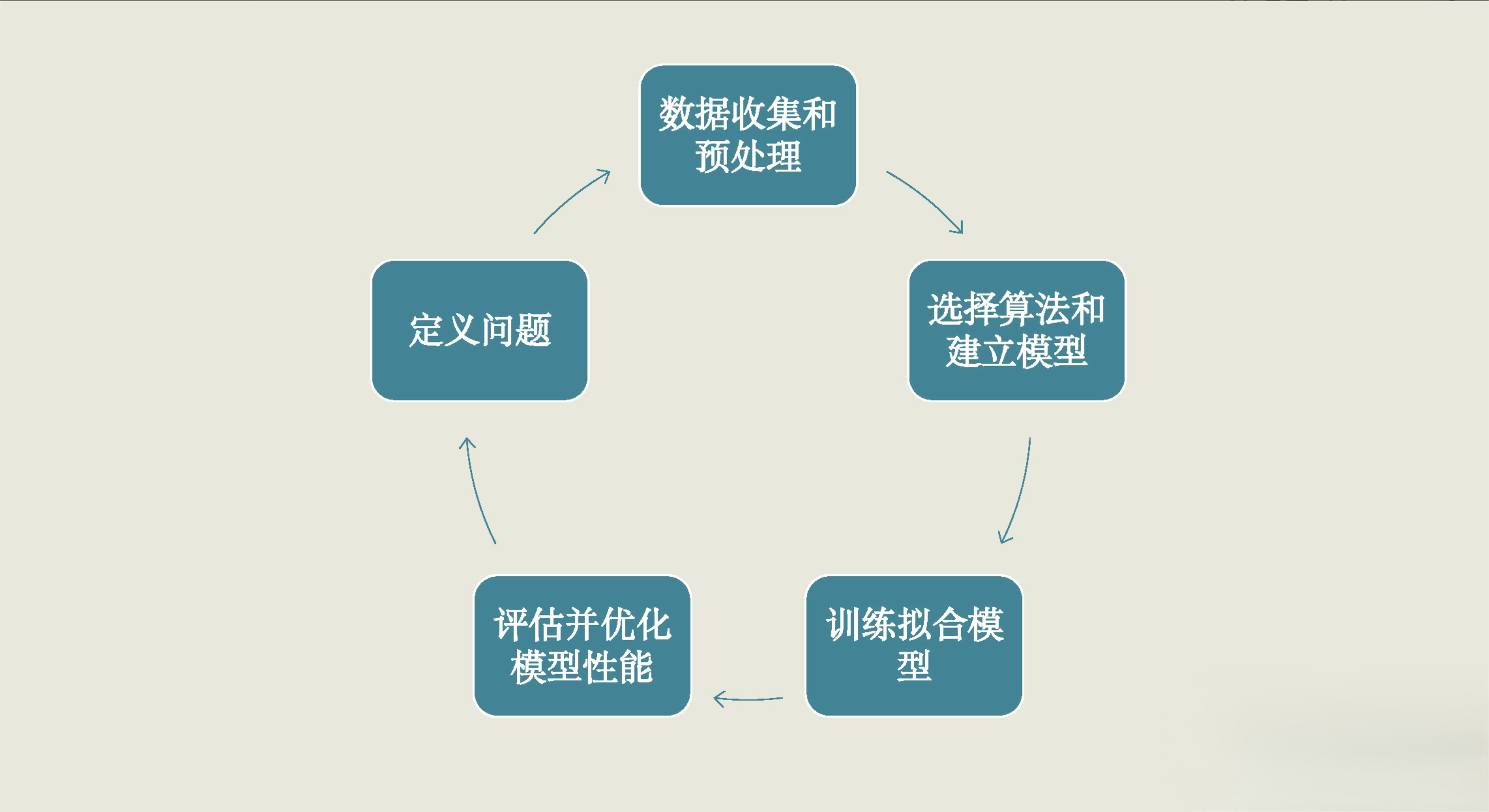
在这“实战 5 步”中,我们每一步做了些什么、机器学习模型做了些什么,都需要你好好地理解和体会。从下一篇开始,我们就要进入更接近实际业务场景的项目实战了,我会引导着你进一步加深对数据和机器学习概念的理解,挖掘出数据之中的价值。
准备好了吗?让我们继续上路,开始正式闯关,在动手实践中把机器学习知识用起来!
思考
在我们这个项目中,使用的是线性回归模型 LinearRegression 的默认外部参数。此时,两个参数的默认值分别是,fit_intercept = True,normalize = False。尽管解释算法中每一个参数的具体意义并非我们的重点,但是阅读算法和参数的说明文档,然后调整参数,优化模型,却是机器学习项目的日常工作。
因此,请你用 fit_intercept 和 normalize 这两个参数练练手,自己调整它们的值,形成各种组合,重新训练出其它外部参数组合的模型。我们可以大概算一下,两个布尔类型参数最多就形成 4 种组合,而且我们的默认参数已经训练出了其中的一种,所以你可以尝试其它三种。
另外,你也可以看一看,对于这个数据集来说,取哪组 fit_intercept 和 normalize 值,你的模型测试结果更优?
最后,给你一个小提示,如果你希望对变量 X 做“规范化”,在建立模型的同时就要指定外部参数 normalize 的值:
from sklearn.linear_model import LinearRegression # 导入线性回归算法模型
linereg_model = LinearRegression(normalize = True) # 使用线性回归算法创建模型,并指定外部参数normalize
补充
在使用GridSearchCV前,需要划分训练集和测试集吗?按照什么比例划分呢?
看到你的答案里面已经用了GridSearchCV。很好,GridSearchCV,默认已经使用了5折交叉验证,就是其中的CV参数。那么我们原来不是说3个集吗,训练集,验证集,测试集。因为GridSearchCV有已经自带交叉验证的存在。就不再需要验证集了。 而测试集,还需要,目的是把GridSearchCV的交叉验证结果拿到测试集做最后测试。
使用了网格搜索自动调参,可以获得更好的预测评分
在方法2我使用了网格搜索自动调参,可以获得更好的预测评分。
# 思考题;
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import GridSearchCV
import pandas as pd
import chardet
import itertools
#查询编码格式
with open('易速鲜花微信软文.csv', 'rb') as f:
enc = chardet.detect(f.read()) # or readline if the file is large
#读取数据
df_ads = pd.read_csv('易速鲜花微信软文.csv', encoding = enc['encoding'])
# 判断空值
df_ads.isna().sum()
# 删掉含空值的行
df_ads = df_ads.dropna()
# 构建特征集和标签集
x = df_ads.drop(['浏览量'], axis = 1)
y = df_ads['浏览量']
# 拆分训练集(80%)和测试集(20%)
xtrain, xtest, ytrain, ytest = train_test_split(x, y, test_size = 0.2, random_state = 0)
# 调参:方法一
fit_intercept_list = [True, False]
normalize_list = [True, False]
print('方法1')
for item in itertools.product(fit_intercept_list, fit_intercept_list):
fit_intercept = item[0]
normalize = item[1]
# 训练模型
linereg_model = LinearRegression(fit_intercept = fit_intercept, normalize = normalize)
linereg_model.fit(xtrain, ytrain)
# 预测测试集对的y值
y_pred = linereg_model.predict(xtest)
# 给出模型评分(使用验证集)
print(f'参数组合; fit_intercept = {fit_intercept},normalize = {normalize}','线性回归预测评分:', linereg_model.score(xtest, ytest))
# 调参:方法2
model = LinearRegression()
# 建立需要搜索的参数的范围
param ={'fit_intercept':[True, False],'normalize': [True, False]}
# 初始化网格搜索的方法
grid = GridSearchCV(model,param)
#用网格搜索方法进行拟合数据
grid.fit(x, y)
# 输出最优的参数组合
print('方法2')
print('最佳模型的参数组合:', grid.best_params_)
print('样本得分平均值:',grid.best_score_)
print('最佳模型测预测评分:',grid.score(xtest, ytest))
#结论:
#1. 最佳参数组合是:{'fit_intercept': True, 'normalize': True} 或 {'fit_intercept': True, 'normalize': False}
#2. 方法2 的预测评分:0.75 高于方法1的预测评分:0.74