问题描述
设计并手动实现一个数据结构,支持 LRU(Least Recently Used,最近最少使用)缓存机制。该结构需要提供以下操作,且两个操作的时间复杂度均为 O(1):
- get(key):如果键存在于缓存中,则返回其对应的值;否则返回 -1。
- put(key, value):如果键不存在,则将其插入缓存并设置为指定的值;如果键已经存在,则更新其值为新值。
当缓存容量已满时,在插入新数据之前,应当删除最近最少使用(即最长时间未被使用)的那一项数据,从而腾出空间。
换句话说,LRU算法会淘汰最近一段时间内最久没有使用过的缓存数据。这种策略假设最近被使用的数据将来被再次访问的可能性更高,而长期未使用的数据被再次访问的可能性更低。
LRU缓存机制解读
LRU 全称是 “Least Recently Used”,中文可直译为最近最少使用。它通过记录数据的使用顺序来决定淘汰哪个缓存项。当缓存满需要淘汰时,会移除那个最近最久未被使用的元素。例如,如果缓存容量为 3,一段时间的操作后缓存中有 A、B、C 三个元素,假设其中 A 是最久未被访问的(即很长时间没用过),而 B 和 C 最近有访问过,那么当需要加入新元素 D 时,就会淘汰 A,保留最近有用到的 B、C,再将新元素 D 加入缓存。
这种策略不同于 LFU(Least Frequently Used,最少使用频率)算法。LRU 根据数据最近是否被访问来进行淘汰决策,而 LFU 则根据数据的访问次数频率来决定淘汰顺序。换言之,LRU关注的是“多久没被使用”,LFU关注的是“被使用了多少次”。理解这一区别很重要,因为错误地将频率当作最近使用程度,可能导致算法不符合同题要求。
常见实现思路
要在 O(1) 时间内完成缓存的读取和更新,我们需要巧妙地选择数据结构。直观来看,使用普通列表或链表存储数据虽然可以按顺序维护元素,但查找某个键是否存在以及删除任意元素可能需要线性时间。相反,哈希表(如 Python 的字典)可以在平均 O(1) 时间内完成查找,但哈希表本身不维护元素的先后使用顺序。因此,实现 LRU 缓存需要将两种数据结构结合:利用哈希表快速定位元素,使用链表维护元素的使用顺序。常见方案是在内部使用一个 哈希表 + 双向链表 来完成这一任务。
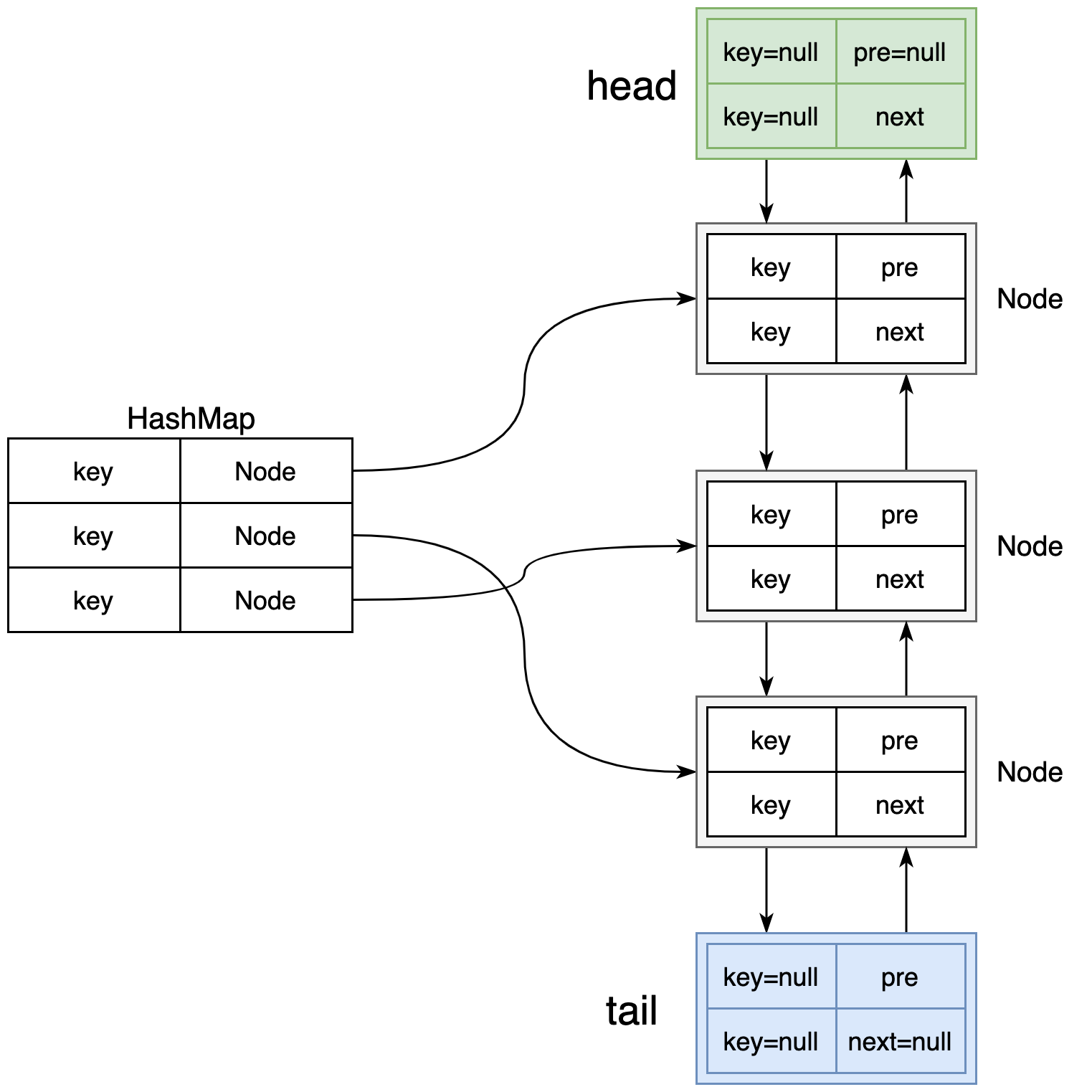
图1:LRU缓存的典型实现结构示意图。
左侧的哈希表(HashMap)通过键快速映射到双向链表的节点位置,
右侧使用双向链表维护缓存项的使用顺序。
链表头部(Head)之后的位置是最近使用的元素,链表尾部(Tail)之前的位置是最久未使用的元素。
当某个键被访问(get 或 put)时,其节点会被移动到链表头部,表示最近被使用;
当缓存容量已满需要淘汰数据时,则从链表尾部删除节点来移除最久未使用的缓存项。
如上图所示,双向链表 和 哈希表 各司其职:
- 双向链表 用于按时间先后维护节点的顺序:越靠近链表头部的节点表示越近期被访问,越靠近尾部则表示越久未被使用。通过双向链表,我们可以在知道节点引用的情况下,在 O(1) 时间内将该节点从链表中移除或移动到头部,因为我们可以直接修改前驱和后继指针,不需要遍历。
- 哈希表(例如 Python 字典)将缓存的 键key 映射到链表中的 节点Node。这样通过键查找对应的缓存值时,可以 O(1) 时间定位到链表里的节点位置。一旦得到节点引用,我们就可以迅速完成更新:如读取后将节点移动到头部,或者删除节点。哈希表避免了遍历链表查找元素的开销。
通过上述结构,get 和 put 操作的逻辑可以简要概括如下:
- get(key): 使用哈希表判断键是否存在。如果存在,定位到对应的节点,取出值返回。同时将该节点从原位置移动到链表头部,表示这一项最近被访问过。若键不存在则返回 -1。
- put(key, value): 先检查键是否已在缓存:
如果在,则更新其值,并将对应节点移动到链表头部(因为最近被访问/更新);
如果不在,则需要新建节点并插入链表头部。
此外,如果缓存已满(当前缓存大小等于容量),则需要淘汰链表尾部的节点(即最久未使用的那项),同时从哈希表中删除对应键。
最后,将新节点插入头部,并在哈希表中添加映射关系。
这种设计确保了 get 和 put 操作都只涉及哈希表的查找/插入/删除(O(1)操作)以及链表的节点插入、删除操作(也是O(1)),完全符合题目要求的时间复杂度。
错误实现的分析
在弄清楚正确方案之前,我们来看一个可能的错误实现,以加深对 LRU 机制的理解。假设有人尝试用一个字典存储缓存,并在字典中记录每个键被访问的次数(使用计数器)来决定淘汰哪一个元素,如下面的伪代码片段所示:
class LRU:
cache = {} # 用于存储缓存数据的字典
max_size = 10 # 缓存容量上限为10
def get(self, key):
if key in self.cache:
value, count = self.cache[key]
# 每次访问,增加计数
self.cache[key] = {value, count + 1}
return self.cache[key] # 返回缓存值
return -1
def put(self, key, value):
# 如果超过容量,移除最近最少使用的项
if len(self.cache) > self.max_size:
min_count = float('inf')
lru_key = None
# 找到使用次数最少的键
for k, (v, count) in self.cache.items():
if count < min_count:
min_count = count
lru_key = k
# 移除使用次数最少的那个键
if lru_key:
self.cache.pop(lru_key)
# 插入新数据(若键已存在则什么都不做)
if key not in self.cache:
self.cache[key] = {value, 0}上述代码尝试满足 LRU 的要求,但存在多个问题:
- 将“最近使用”误解为“使用频率”:代码里维护的
count是键被访问的次数。这实际上对应的是 LFU(最少使用频率)策略,而非 LRU。LRU要求淘汰的是最久没被访问的元素,而不是访问次数最少的元素。举个例子,假设缓存容量为 2,序列操作为:put(A),put(B),get(A),put(C)。此时 A 被访问过一次,B 从未被访问过。根据 LRU,应淘汰 B(因为 B 比较久没被用了);但上述实现中,A 的访问次数为1,B的访问次数为0,算法会错误地淘汰访问次数更少的 A。这与 LRU 理念不符。 - 无法真正记录“最近最少使用”:要正确记录最近使用的顺序,关键是在每次访问时更新元素的位置或时间戳。上述代码只是增加计数,却没有任何机制区分“最近一次访问发生在什么时候”。例如,元素的
count可能因为多次集中访问变得很高,但之后长时间不再被访问。根据 LRU,它可能变成淘汰候选,但单凭一个累计次数无法判断这一点。LRU需要追踪访问的时序,而非简单计数。 - 字典迭代删除的效率问题:代码在插入时,如果超过容量,会遍历整个
self.cache找出count最小的键来删除。这一步需要 O(n) 时间(n为缓存大小)。若缓存很大,这种做法在频繁插入时性能会很差,无法满足 O(1) 操作要求。正确的实现中,我们应当直接找到最久未使用的节点,而不是每次扫描所有元素。 - Python 实现细节错误:从代码细节看,还有一些错误之处。例如,用
{value, count}来存储值和计数,这是在创建集合(set)而非元组,取出数据顺序无法保证,而且get方法中return self.cache[key]返回的将是一个集合对象而不是实际的值。本应直接返回缓存的值部分。另外,类变量cache = {}会被所有实例共享,并且可能导致意外的状态持久(应该使用实例变量self.cache)。这些实现细节的问题虽然不属于算法思想的错误,但也需要修正。
综合以上分析可知,基于访问次数的方案并不适用于 LRU,要实现真正的 LRU,我们需要按访问时间先后来维护缓存项顺序。接下来,我们将按照正确的思路一步步设计并实现一个满足要求的 LRU 缓存。
正确的 LRU 缓存实现方案
如前文所述,实现 LRU 缓存需要组合使用哈希表和双向链表。下面我们详细说明设计思路:
- 双向链表维护使用顺序:我们以双向链表保存缓存中的键值对节点,每当某个键被访问时,就将该节点移到链表的头部,表示“最近使用”;链表尾部的节点则代表“最久未使用”。这样,链表尾部元素就是需要淘汰的候选。双向链表允许我们在已知节点的情况下,在 O(1) 时间内将其插入或移除(只需修改相邻节点的指针),非常适合频繁的节点移动操作。
- 哈希表快速定位节点:使用哈希表(如字典)存储键到链表节点的映射关系。通过键我们可以 O(1) 时间找到对应的节点对象,从而对其进行移动或删除,而无需遍历链表。哈希表保证了
get操作能快速找到值,put操作能快速检查键是否存在,以及在淘汰节点时可以快速通过键从表中删除它。
基于以上结构,容量为 N 的缓存在最坏情况下空间复杂度为 O(N)(存储 N 个节点和 N 个哈希映射项)。get 和 put 操作的时间复杂度如下:
- get: O(1) 时间内通过哈希表找到节点,再将节点移动到头部,操作指针也是 O(1)。
- put: O(1) 时间检查存在性和容量;如果需要淘汰,从链表尾部删除节点是 O(1),从哈希表删除对应键也是 O(1);插入新节点到头部和在哈希表中添加键也是 O(1)。
接下来,我们按照这一设计实现具体的代码(使用 Python 伪代码展示关键逻辑,并给出详细注释)。
LRU缓存的代码实现(Python)
我们将实现一个 LRUCache 类,其构造函数接受一个正整数作为容量 capacity。内部使用一个双向链表和一个字典来维护缓存状态。为方便操作链表,我们引入一个辅助的双向链表节点类 DLinkedNode,每个节点存储键、值以及前驱和后继指针。
class DLinkedNode:
def __init__(self, key=None, value=None):
self.key = key # 键
self.value = value # 值
self.prev = None # 前驱指针
self.next = None # 后继指针
class LRUCache:
def __init__(self, capacity: int):
self.capacity = capacity # 缓存容量
self.cache = dict() # 哈希表:键 -> 对应的节点
# 创建双向链表的伪头部和伪尾部(哨兵节点),简化节点插入和删除逻辑
self.head = DLinkedNode() # 伪头节点(不存储实际数据)
self.tail = DLinkedNode() # 伪尾节点(不存储实际数据)
self.head.next = self.tail
self.tail.prev = self.head
def _add_node(self, node: DLinkedNode):
"""将新节点加入双向链表的头部(紧贴着伪头节点之后)"""
node.prev = self.head
node.next = self.head.next
self.head.next.prev = node # 原本head之后的第一个节点的前驱更新为node
self.head.next = node # head的后继更新为新节点
# 新节点现在成为链表的实际第一个数据节点(位于伪头之后)
def _remove_node(self, node: DLinkedNode):
"""从双向链表中移除一个节点"""
prev = node.prev
nxt = node.next
prev.next = nxt
nxt.prev = prev
# 被移除的node前后指针将会被垃圾回收回收(或可手动置None以防误用)
def _move_to_head(self, node: DLinkedNode):
"""将链表中的指定节点移动到头部(表示最近使用)"""
self._remove_node(node) # 从原位置移除
self._add_node(node) # 再插入到头部
def _pop_tail(self) -> DLinkedNode:
"""弹出链表尾部的真实节点(最久未使用的节点)"""
node = self.tail.prev # 取出伪尾节点前的最后一个真实节点
self._remove_node(node) # 将其从链表中移除
return node # 返回该节点
def get(self, key: int) -> int:
if key not in self.cache:
return -1
node = self.cache[key] # 通过哈希表定位节点
# 移动该节点到链表头部,表示这个节点最近被访问过
self._move_to_head(node)
return node.value
def put(self, key: int, value: int) -> None:
if key in self.cache:
# 若键已存在,找到节点,更新其值并移到头部
node = self.cache[key]
node.value = value # 更新值
self._move_to_head(node)
else:
# 若键不存在,创建新节点
node = DLinkedNode(key, value)
# 将新节点添加到链表头部
self._add_node(node)
# 在哈希表中添加键映射到该节点
self.cache[key] = node
# 如果超过容量,则淘汰尾部节点
if len(self.cache) > self.capacity:
# 弹出最久未使用的节点(链表尾部)
tail_node = self._pop_tail()
# 从哈希表中删除对应的键
self.cache.pop(tail_node.key, None)上述代码实现了一个简化的 LRU 缓存,各方法说明如下:
_add_node(node):将传入的节点插入到双向链表头部。由于我们使用了伪头节点self.head,新节点会插入在self.head之后成为新的第一元素。时间复杂度 O(1)。_remove_node(node):断开传入节点与链表的连接,将其前驱和后继互相连接起来,从而将该节点移出链表。时间复杂度 O(1)。_move_to_head(node):调用上述两个方法的组合,实现“将已有节点移动到头部”的效果。即先移除,再作为新节点插入头部。时间复杂度 O(1)。_pop_tail():找到链表尾部的最后一个数据节点(伪尾前的节点),将其移除并返回。这就是最久未使用的缓存节点。时间复杂度 O(1)。get(key):首先通过字典检查键是否存在。如果不存在返回 -1;如果存在,则通过字典拿到对应节点,返回其值之前,先调用_move_to_head(node)将该节点移动到链表头部,因为一次访问意味着它成为最近使用的节点。整个过程查找哈希表 O(1),移动节点 O(1)。put(key, value):分为两种情况处理。若键已在缓存中,直接更新对应节点的值,并将该节点移动到头部(因为更新也算一次使用)。若键不在缓存,则创建新节点并插入头部,同时在字典中记录该键。如果此时缓存大小超过容量,则调用_pop_tail()移除链表尾部最久未使用的节点,并从字典中删除那个节点的键。这样腾出空间后将新节点插入。整个过程中新节点插入和字典操作是 O(1);可能触发的淘汰也是 O(1)。
通过上述逻辑,我们已经完整地实现了 LRU 缓存的机制:每次访问会更新使用顺序,每次插入会维护容量限制并淘汰最久未使用的数据。这满足了题目的要求。下面我们通过一个具体的操作序列,看看缓存内容的演变过程。
示例演示
假设我们创建一个容量为 2 的 LRUCache,并进行一系列操作:
cache = LRUCache(2) # 缓存容量 2
cache.put(1, 100) # 插入键1,值100
cache.put(2, 200) # 插入键2,值200
cache.get(1) # 访问键1,返回100
cache.put(3, 300) # 插入键3,值300(此时容量满,需要淘汰一个键)
cache.get(2) # 尝试访问键2
cache.get(3) # 访问键3
cache.get(1) # 再次访问键1让我们逐步分析发生了什么:
- 初始状态:缓存为空。
put(1,100): 插入键1。缓存现在包含 {1=100}。链表: 1(最近) -> NULL。put(2,200): 插入键2。缓存包含 {1=100, 2=200}。链表更新为 2(最近), 1(最久)。因为刚插入2,把2放在头部表示最近使用,1在后面。get(1): 键1存在,返回100。访问键1后,要将键1对应节点移到头部。链表顺序变为 1(最近), 2(最久)。put(3,300): 插入新键3,容量将超出2,因此需要淘汰一个。根据链表,当前最久未使用的是键2(在尾部),于是键2被移除。随后插入键3到头部。此时缓存包含 {1=100, 3=300}。链表顺序:3(最近), 1(最久)。键2已被淘汰。get(2): 查找键2,发现已被淘汰,不在缓存中,返回 -1。缓存状态不变。get(3): 键3存在,返回300。访问后将键3节点移到头部(不过键3本来就在头部,因为它刚刚被插入且之后没有更久的访问)。缓存仍为 {1=100, 3=300},链表顺序仍是 3(最近), 1(最久)。get(1): 键1存在,返回100。访问后将键1节点移到头部。现在链表顺序变为 1(最近), 3(最久)。缓存内容未变 {1=100, 3=300}。
通过这个例子可以看到,LRUCache 会根据最近的访问情况动态调整顺序,并在需要的时候淘汰正确的元素。整个过程中,每一步操作,我们的实现都在 O(1) 时间内完成了。
总结
LRU 缓存机制通过淘汰最近最少使用的数据,保证了经常使用的数据能够保留在缓存中,从而提高命中率。在实现方面,借助哈希表和双向链表的组合,我们可以高效地完成这一策略,使得缓存的读取和更新操作都达到 O(1) 时间复杂度。关键在于用双向链表维护“最近使用”的顺序,用哈希表快速查找需要的元素位置。
需要注意的是,不要将 LRU 与 LFU 混淆。LRU关注的是时间维度的“最近使用”,LFU关注的是次数维度的“使用频率”。实现时也应避免仅用计数器等简单方法尝试替代时间顺序的维护,否则会偏离题意。
在实际开发中,各种语言和框架也常提供了现成的 LRU 实现或容器,例如 Java 的 LinkedHashMap 可以很方便地构建 LRUCache,Python 中有 collections.OrderedDict(在 Python3.7+字典本身也是有序的)或 functools.lru_cache 装饰器等。不过,在面试或算法题环境下,要求我们手动实现LRU,则更看重对底层原理的掌握和代码细节的处理。通过以上的分析与实现,我们详细了解了 LRU 缓存的工作机制和正确的实现方法,希望这对你深入理解 LRU 算法有所帮助。